江戸時代の和算家、村松茂清の円周率計算をC++プログラム化する

日本で初めて円周率を求める数学的アルゴリズムを提示したのは、村松茂清の算俎（1663年）と言われている（平山諦「学術を中心とした和算史上の人々」（1965年刊）による）。これをコンピュータプログラム上で再現してみるのが今回の狙いだ。

まず、初めにそのアルゴリズムそのものをここに示しておく。

原著の算俎では、この辺り https://kotenseki.nijl.ac.jp/biblio/100248259/viewer/137 に書かれていると思われるが、現状では読みきれない。

そこで、平山氏の著作に詳しい記載があり、また、私自身の理解のために、筑波大学の礒田正美氏のサイトにある数学史の教育素材「和算入門　第壱章　算木」を参考にさせていただいた。それらをもとに、アルゴリズムを再現すると、以下のようになる。

 

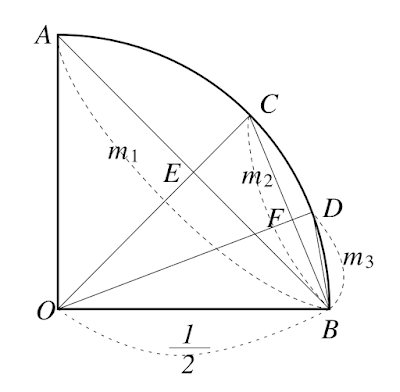
図のように、直径一の円の四分の一を考える。ACDBは円弧上にあり、角AOBは直角である。円弧ABは円の四分の一、円弧CBは円の八分の一、円弧DBは円の十六分の一である。このように、円弧の長さを半分ずつにしていく。そして、求めたmiを、円全体に内接するように整数倍すれば、その長さが円周率になるわけである。

まず、四分の一の場合から求める。ABの長さm1は、直角二等辺三角形の斜辺であるから、m1=√2/2である。m2は、ピタゴラスの定理によりCEの二乗とBEの二乗の平方根である。CEの長さは、COの長さすなわち、√2/2からOEを引いたものであり、OEはBEに等しく、BEは、ちょうどm1の半分である。これでm2が求められる。

m3の長さも、m2が求められた後では、BFの長さが、m2の半分であり、OBが1/2であることから、OFが求められ、したがって、FDが求められ、BFの二乗とFDの二乗の平方根がm3になるので、求めることができる。

以上の手続きから、一般にmiとmi-1の関係として表すと次のようになる。

これをC++のプログラムにすると以下のようになる。

/*                                                                                                           
村松茂清の方法による円周率の計算                                                                             
2021年2月18日                                                                                                
 */
#include <iostream>
#include <iomanip>
using namespace std;

int main(){
  cout << fixed << setprecision(30);
  long double m = sqrtl(2.0)/2.0, t = 2.0;
  long double pi;
  long double s1,s2;
  for (int n=1; n<50; n++)
    {
      t*=2.0;
      pi= t*m;
      cout << "n = " << n << " m = " << m << " pi = " << pi << endl;
      s1 = (m/2.0)*(m/2.0);
      s2 = sqrtl(0.25-s1);
      m = sqrtl((0.5-s2)*(0.5-s2)+s1);
    }
}

計算結果は次のようになる。

アルゴリズムそのものは正しいはずだが、n=31までは、改善がある。

 3.141592653589793238

それ以後は改良が無くなった。コンピュータの計算精度の問題だと思う。どなたかご教示いただければ幸いである。

しかし、このn=1の時は、四角形を内接させて計算させているが、n=31の時は、4,294,967,296角形、約43億角形を内接させているので、人間の目にはほぼ完全な円に見えているはずである。

ちなみに、村松茂清は、32,768角形まで計算したようだ。それでも、手計算でやったことを考えれば、驚異的なものだと思う。